Obliczanie stanu generatora liczb pseudolosowych – na przykładzie Math.random() z Firefoksa

Inspiracja

Bezpośrednią inspiracją do napisania tego artykułu było zadanie random4 z bardzo ciekawego zestawu łamigłówek return true to win. Każde zadanie zawiera krótki fragment kodu ze zdefiniowaną funkcją zwracającą wartość boolowską. Zadaniem rozwiązującego jest przekazanie takich parametrów do funkcji, aby zwróciła ona wartość true. Nie zawsze jest to proste, zazwyczaj wymaga znajomości niuansów standardu ECMAScript lub, idąc jeszcze dalej, specyficznych cech JavaScriptu w przeglądarkach. Polecam spróbować zmierzyć się z tymi zadaniami, bo pozwalają lepiej poznać najistotniejszy język programowania świata webu.

Wróćmy jednak do zadania random4. Kod wyglądał następująco:

var rand = Math.random();
function random4(x) {
  return rand === x;
}

Jak widzimy, do zmiennej rand przypisywana jest wartość losowa wygenerowana przez Math.random(). W kolejnym kroku, musimy wywołać funkcję random4 z takim parametrem, żeby zwróciła ona true. Innymi słowy, nasz parametr musi być równy wcześniejszej wartości Math.random()… Gdy już wszystkie pomysły zawiodły i wyglądało na to, że nie wchodzi tutaj w grę żadna specyficzna cecha Javascriptu (lub błąd w przeglądarce), zadanie sprowadziło się do innego problemu: trzeba ustalić stan generatora liczb pseudolosowych!

Jak działają generatory liczb pseudolosowych

Pomijając zastosowania kryptograficzne, gdzie wiele uwagi poświęca się temu, by liczby losowe były w istocie losowe, w pozostałych dziedzinach mamy zazwyczaj do czynienia z liczbami pseudolosowymi. Metody generowania liczb pseudolosowych są różne – w zależności od tego z jakiego skorzystamy algorytmu – ale zasadniczo sprowadzają się do kilku kroków:

1. Do generatora liczb pseudolosowych przekazujemy ziarno (ang. seed). W ten sposób ustalany jest stan (ang. state) generatora.
2. Generator wykonuje operacje arytmetyczne, na podstawie których oblicza nową wartość stanu.
3. Na podstawie stanu generatora, wyliczana jest nowa wartość pseudolosowa.

Charakterystyczną cechą generatorów liczb pseudolosowych jest fakt, że podanie tego samego ziarna skutkuje wygenerowaniem takiej samej sekwencji liczb.

Generatory liczb pseudolosowych w przeglądarkach

We wszystkich najpopularniejszych przeglądarkach internetowych (czyli w Chromie, Firefoksie oraz Edge’u) stosowany jest ten sam algorytm generowania liczb pseudolosowych: XorShift128+. W dalszej części tekstu będę jednak odnosił się wyłącznie do implementacji z Firefoksa ze względu na fakt, że jest ona – moim zdaniem – najczytelniejsza.

Zobaczmy więc odpowiedni fragment kodu z silnika Gecko:

XorShift128PlusRNG(uint64_t aInitial0, uint64_t aInitial1) {
  setState(aInitial0, aInitial1);
}

uint64_t next() {
  uint64_t s1 = mState[0];
  const uint64_t s0 = mState[1];
  mState[0] = s0;
  s1 ^= s1 << 23; mState[1] = s1 ^ s0 ^ (s1 >> 17) ^ (s0 >> 26);
  return mState[1] + s0;
}

Jak widać w powyższym kodzie, stan generatora XorShift128+ składa się z dwóch liczb 64-bitowych. Zaś obliczenie kolejnej liczby pseudolosowej polega na przeliczeniu nowej wartości jednej z liczb stanu (co sprawdza się do kilku przesunięć bitowych oraz operacji XOR), a następnie dodaniu do siebie dwóch liczb stanu.

Wnikliwi czytelnicy zauważą, że XorShift128+ generuje 64-bitowe liczby całkowite, zaś funkcja Math.random() zwraca liczbę zmiennoprzecinkową z zakresu [0, 1). Jak więc ten uint64_t jest zamieniany na double? Na to pytanie odpowiada kolejna funkcja ze źródeł: nextDouble.

double nextDouble() {
  static constexpr int kMantissaBits =
mozilla::FloatingPoint::kExponentShift + 1;
  uint64_t mantissa = next() & ((UINT64_C(1) << kMantissaBits) - 1);
  return double(mantissa) / (UINT64_C(1) << kMantissaBits);
}

Kod sprowadza się się do tego, że z wygenerowanej wartości 64-bitowej pobierane są 53 najmłodsze bity, które następne są dzielone przez 2⁵³. W ten sposób mamy gwarancję, że dostaniemy liczbę z zakresu [0,1). Nie było sensu brać do dzielenia większej liczby bitów, ponieważ typ danych double nie jest i tak w stanie pomieścić większej precyzji.

Jako proste ćwiczenie, będące bazą do naszych dalszych operacji, przepiszmy kod generujący liczby pseudolosowe do Pythona.

class XorShift128PlusFirefox(object):
    def __init__(self, s0, s1):
        self.s0 = s0
        self.s1 = s1
        self.state = [s0, s1]
        
    def next(self):
        s1 = self.state[0]
        s0 = self.state[1]
        
        self.state[0] = s0
        s1 ^= (s1 << 23)
        s1 &= 0xffffffffffffffffL
        self.state[1] = s1 ^ s0 ^ (s1>>17) ^ (s0>>26)
                
        random_val = (self.state[1] + s0) & 0xffffffffffffffffL 
        
        return random_val
    
    def next_double(self):
        return float(self.next() & 0x1fffffffffffffL) / 2**53

Powyższy kod jest praktycznie dosłownym przełożeniem kodu C++ na Pythona. Klasa XorShift128PlusFirefox w konstruktorze przyjmuje dwie wartości określające stan generatora; funkcja next() pozwala wygenerować kolejną 64-bitową liczbę całkowitą, zaś next_double() – kolejną liczbę typu zmiennoprzecinkowego z zakresu [0,1).

Przykładowe użycie klasy XorShift128PlusFirefox możemy zobaczyć na Rys 1. Wygenerowane zostały dwie liczby pseudolosowe na podstawie podanego stanu.

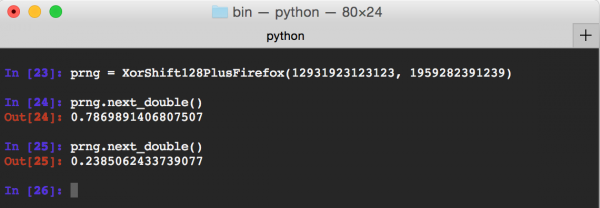
Rys 1. Wygenerowanie dwóch liczb losowych algorytmem XorShift128+

Narzędzie Z3Prover

Wiemy już jak działa generator liczb losowych w Firefoksie, napisaliśmy nawet jego implementację w Pythonie. Powoli zbliżamy do meritum tego tekstu, czyli do ustalania stanu generatora na podstawie znajomości kilku jego liczb. Wcześniej jednak poznajmy narzędzie, dzięki któremu uda nam się to osiągnąć: Z3Prover.

Z3Prover to narzędzie klasy SMT solver – pozwala na automatyczne dowodzenie twierdzeń. Krótko mówiąc: narzędzie jako wejście przyjmuje zestaw warunków logicznych (które mogą składać się między innymi z operacji arytmetycznych oraz bitowych), a następnie próbuje przeliczyć, czy istnieją dane wejściowe, dla których te warunki są spełnione. Kilka przykładów zobaczymy poniżej.

Aby móc zacząć używać Z3Prover, należy najpierw skompilować jego źródła lub pobrać pliki binarne. Polecam użyć tej drugiej opcji. Po rozpakowaniu plików binarnych, należy uruchomić Pythona w tym samym katalogu, w którym zostały one rozpakowane i wywołać polecenie:

from z3 import *
# lub alternatywnie
import z3

Przykład 1

Zaczynamy od trywialnego przykładu: definiujemy dwa symbole, będące zmiennymi boolowskimi, i sprawdzamy kiedy ich koniunkcja będzie równa prawdzie. Oczywiście z3 zwraca nam odpowiedź, że równanie jest spełnione, gdy obie zmienne są prawdziwe.

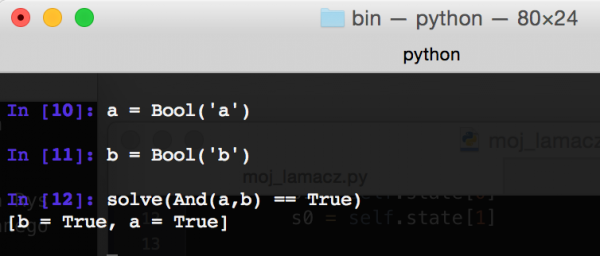
Rys 2. Proste użycie z3

Przykład 2

W z3 możemy również operować na liczbach. W tym przykładzie zdefiniowaliśmy dwie liczby całkowite, a następnie próbujemy rozwiązać równanie: 4*a+7*b=9 przy założeniu, że a<5 oraz b>a.

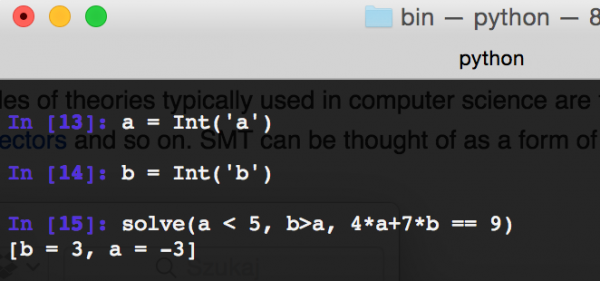
Rys 3. Operowanie na liczbach całkowitych w z3

Przykład 3

Kolejnym typem danych, który poznajemy jest BitVec – jest to liczba całkowita o zadanej przez nas liczbie bitów. Następnie próbujemy rozwiązać równanie, w którym łączymy ze sobą zarówno operatory bitowe, jak i arytmetyczne.

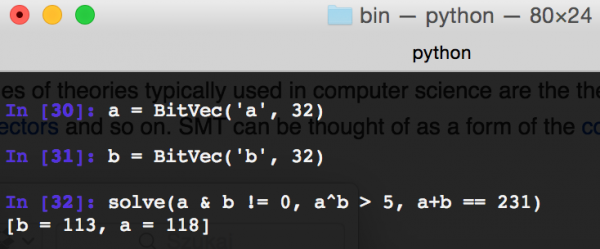
Rys 4. Operowanie na liczbach o określonej liczbie bitów

Przykład 4

Z3 można równie dobrze wykorzystać do upraszczania pewnych wyrażeń w postaci symbolicznej, zamiast ich obliczania.

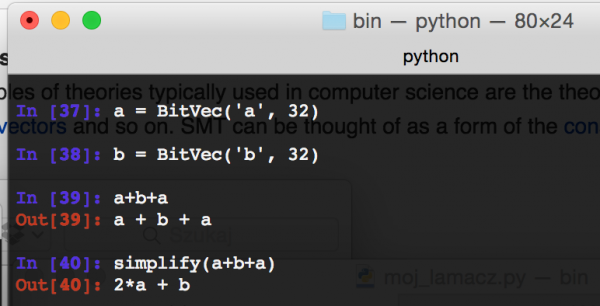
Rys 5. Wykorzystanie z3 do upraszczania wyrażeń

„Łamanie” generatora liczb

Nadeszła pora na napisanie „łamacza” generatora liczb losowych, co sprawdza się do kilku elementów:

• Za pomocą z3 zapiszemy postać symboliczną trzech kolejnych liczb losowych generowanych algorytmem XorShift128+,
• Trzy kolejne liczby zmiennoprzecinkowe wygenerowane przez Math.random() zamienimy na liczby całkowite,
• Na podstawie powyższych danych, wygenerujemy trzy równania ze zmiennymi s0 i s1, których rozwiązanie pozwoli nam ustalić stan generatora liczb pseudolosowych.

Zacznijmy więc od podstawowych definicji:

class Cracker(object):
    def __init__(self, known_values):
        # zmienne stanu to dwie liczby 64-bitowe
        self.s0 = z3.BitVec('s0', 64)
        self.s1 = z3.BitVec('s1', 64)
        self.state = [self.s0, self.s1]
        
        # klasa Solver to klasa, do której możemy dodawać
        # równania, które docelowo będziemy chcieli rozwiązać
        self.solver = z3.Solver()
        
        # zmienna known będzie zawierała znane wartości
        # liczb pseudolosowych wygenerowane w Firefoksie
        self.known = known_values

Mamy klasę Cracker, w której definiujemy zmienne s0 i s1 zawierające stan generatora oraz zmienną state zawierającą to samo, ale w postaci tablicy. Pole solver przechowuje klasę Solver z z3, która przyjmuje równania do rozwiązania. Do pola known z kolei przekażemy znane wartości liczb pseudolosowych, które wygenerujemy dzięki metodzie Math.random() z Firefoksa.

Zaimplementujmy więc metodę next() generatora:

    def next(self):
        s1 = self.state[0]
        s0 = self.state[1]
        
        self.state[0] = s0
        s1 ^= (s1 << 23)
        self.state[1] = s1 ^ s0 ^ z3.LShR(s1,17) ^ z3.LShR(s0,26)
                
        return self.state[1] + s0

Metoda next() wygląda właściwie identycznie jak w oryginalnym kodzie Firefoksa. Jedyną różnicą jest zastosowanie funkcji z3.LShR zamiast operatora >>. Wynika to z faktu, że w z3 operator >> jest arytmetycznym przesunięciem bitowym w prawo. Co za tym idzie, jeżeli bit znaku będzie równy 1, to zostanie on zachowany. LShR to z kolei logiczne przesunięcie bitowe w prawo, które zapewnia nam, że najstarszy bit będzie zawsze ustawiony na 0.

Zobaczmy, z ciekawości, jak w postaci symbolicznej wyglądają liczby losowe po dwóch pierwszych wywołaniach funkcji next() (Rys 6.)

Rys 6. Dwa pierwsze wywołania next() w postaci symbolicznej

Po pierwszym wywołaniu next() postać symboliczna jest niemal dokładnie taka sama jaką widzieliśmy w kodzie tej metody. Po drugim wywołaniu sytuacja zaczyna się już bardziej komplikować: widzimy bardziej zawiły opis liczby, choć nadal jedynymi zmiennymi, do których się on odnosi są s0 i s1.

Teraz wygenerujemy w Firefoksie trzy liczby losowe, przy czym:

• Pierwsza liczba losowa będzie równa postaci symbolicznej liczby po pierwszym wywołaniu next(),
• Druga liczba losowa będzie równa postaci symbolicznej liczby po drugim wywołaniu next(),
• Trzecia liczba losowa będzie równa postaci symbolicznej liczby  po trzecim wywołaniu next().

Do rozwiązania pozostał nam jeden istotny problem: funkcja next() zwraca liczbę w postaci uint64_t, zaś z Firefoksa dostaniemy liczby zmiennoprzecinkowe. Będziemy musieli więc musieli je przekształcić z powrotem na liczby całkowite. To jednak nie będzie trudne. Jak pamiętamy Firefox wyciągał z 64-bitowej liczby jej 53 najmłodsze bity, a następnie dzielił przez 2⁵³. Więc my po prostu odwrócimy ten proces. Liczbę, którą dostaniemy z Firefoksa pomnożymy przez 2⁵³, a z liczby, którą będziemy mieli w postaci symbolicznej, wyciągniemy tylko 53 bity. W efekcie dostaniemy dwie 53-bitowe liczby całkowite do porównania. Popatrzmy na kod samego „łamacza”:

    def crack(self):
        for val in self.known:
            self.solver.add((self.next() & 0x1fffffffffffff) == long(val * 2**53))
        if self.solver.check() != z3.sat:
            raise("Not solved!")
        
        model = self.solver.model()
        s0 = model[self.s0].as_long()
        s1 = model[self.s1].as_long()
        
        return (s0, s1)

W powyższym kodzie iterujemy po znanych wartościach liczb losowych. Wartości typu double mnożymy przez 2⁵³ i porównujemy je z 53 najmłodszymi bitami liczby wygenerowanej przez wywołanie next(). Takie równania wrzucamy do solvera z z3. Następnie wywołujemy metodę solver.check() rozwiązującą podane przez nas równania. Jeżeli metoda zwróci wartość z3.sat, to oznacza, że równania udało się rozwiązać. Wyliczone wartości możemy pobrać odwołując się do modelu. Ostatecznie, funkcja zwraca wartości s0 i s1 będące stanem generatora liczb losowych.

Wygenerowałem więc w Firefoksie trzy kolejne liczby losowe:

• 0.8629073810129263,
• 0.19187870241845773,
• 0.07371019627869657.

Zobaczmy, czy nasz Cracker będzie w stanie ustalić stan generatora (Rys 7.).

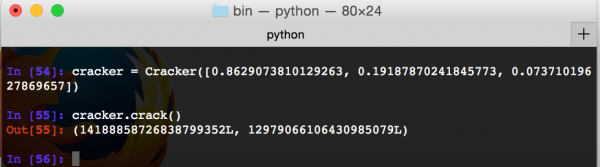
Rys 7. Ustalenie stanu generatora na podstawie trzech liczb

Sukces! Dzięki z3 odtworzyliśmy stan generatora. Spróbujmy teraz wykorzystać ten stan jako argument do wcześniej napisanego przez nas generatora (klasa XorShift128PlusFirefox) i zobaczmy, czy rzeczywiście wygeneruje takie same liczby (rys 8).

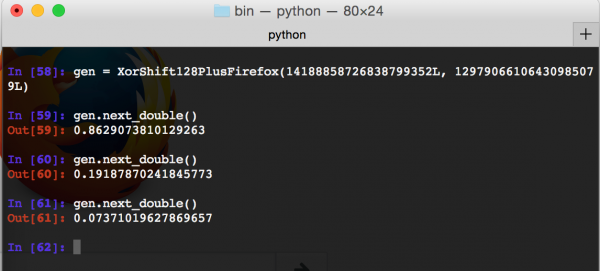
Rys 8. Wykorzystanie obliczonego stanu do ponownego wygenerowania liczb

Dostaliśmy taką samą sekwencję, jaką wygenerował Firefox, co pokazuje, że nasza pythonowa implementacja łamania i generowania kolejnych liczb pseudolosowych jest poprawna.

Rozwiązanie problemu z zadania random4

Pozostaje więc rozwiązać problem ze wspomnianego na początku zadania random4. Ze względu na specyfikę tamtego zadania, my mogliśmy wygenerować dowolnie dużo liczb losowych, jednak musieliśmy ustalić jaka liczba została wygenerowana przed naszymi wywołaniami Math.random(). Okazuje się, że przy aktualnym kodzie rozwiązanie takiego problemu jest łatwe: po przeliczeniu stanu generatora, nie będziemy wywoływać metody next() (ona powoduje bowiem obliczenie nowego stanu), tylko wygenerujemy liczbę na podstawie stanu, który znamy.

Poniżej pełny kod rozwiązania – zmiany opisane w akapicie powyżej są odzwierciedlone w metodzie current_double(). Ponadto został dodany kod, dzięki któremu do skryptu pythonowego można przekazać argument zawierający trzy oddzielone od siebie przecinkami liczby wygenerowane w Math.random().

# -*- coding: utf-8 -*-
import z3
import sys

class XorShift128PlusFirefox(object):
    def __init__(self, s0, s1):
        self.s0 = s0
        self.s1 = s1
        self.state = [s0, s1]
    
    def current_double(self):
        val = (self.s0 + self.s1) & 0x1fffffffffffffL
        return float(val) / 2**53
    
    def next(self):
        s1 = self.state[0]
        s0 = self.state[1]
        
        self.state[0] = s0
        s1 ^= (s1 << 23)
        s1 &= 0xffffffffffffffffL
        self.state[1] = s1 ^ s0 ^ (s1>>17) ^ (s0>>26)
                
        random_val = (self.state[1] + s0) & 0xffffffffffffffffL 
        
        return random_val
    
    def next_double(self):
        return float(self.next() & 0x1fffffffffffffL) / 2**53
    
class Cracker(object):
    def __init__(self, known_values):
        # Zmienne stanu to dwie liczby 64-bitowe.
        self.s0 = z3.BitVec('s0', 64)
        self.s1 = z3.BitVec('s1', 64)
        self.state = [self.s0, self.s1]

        # Klasa Solver to klasa, do której możemy dodawać
        # równania, które docelowo będziemy chcieli rozwiązać
        self.solver = z3.Solver()

        # Zmienna known będzie zawierała znane wartości
        # liczb pseudolosowych wygenerowane w Firefoksie.
        self.known = known_values
    
    def next(self):
        s1 = self.state[0]
        s0 = self.state[1]
        
        self.state[0] = s0
        s1 ^= (s1 << 23)
        self.state[1] = s1 ^ s0 ^ z3.LShR(s1,17) ^ z3.LShR(s0,26)
                
        return self.state[1] + s0
    
    def crack(self):
        # Ze względu na sposób generowania liczb w Firefoksie,
        # z obliczonej przez z3 liczby pobieramy tylko 53 najmłodsze
        # bity. Z kolei liczbę zmiennoprzecinkową zamieniamy na
        # całkowitą poprzez pomnożenie jej przez 2**53.
        for val in self.known:
            self.solver.add((self.next() & 0x1fffffffffffff) == long(val * 2**53))
        if self.solver.check() != z3.sat:
            raise Exception("Not solved!")
        
        model = self.solver.model()
        s0 = model[self.s0].as_long()
        s1 = model[self.s1].as_long()
        
        return (s0, s1)

def main():
    # Pobieramy z linii poleceń jeden argument reprezentujący
    # kilka liczb zmiennoprzecinkowych oddzielonych przecinkami.
    known_values = [float(v) for v in sys.argv[1].split(",")]
    
    # "Łamiemy" stan generatora liczb losowych.
    cracker = Cracker(known_values)
    (s0, s1) = cracker.crack()
    
    # Wykorzystujemy obliczony stan generatora do obliczenia
    # poprzedniej liczby pseudolosowej.
    prng = XorShift128PlusFirefox(s0, s1)
    print "{:.16}".format(prng.current_double())

if __name__ == '__main__':
    main()

Jako ostateczny test poprawności rozwiązania: wygeneruję w Firefoksie cztery kolejne liczby pseudolosowe, przekażę trzy ostatnie do crackera i zobaczę, czy zostanie wygenerowana ta pierwsza (Rys 8.).

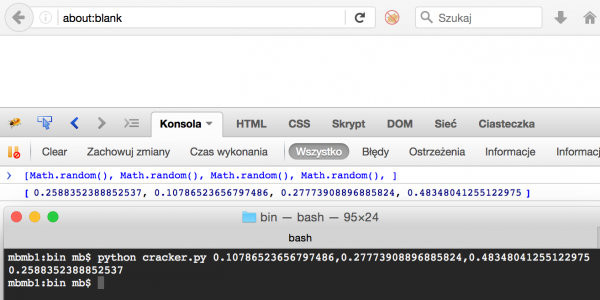
Rys 8. Ostateczny test crackera

Podsumowanie

We wszystkich popularnych dzisiaj przeglądarkach internetowych generowanie liczb pseudolosowych odbywa się z użyciem algorytmu XorShift128+. Generowanie kolejnych liczb polega na wykonaniu kilku prostych operacji arytmetyczno-logicznych, a co za tym idzie znając kilka kolejnych liczb, możemy ustalić stan generatora co pozwoli zarówno na przeliczenie jakie liczby zostaną wygenerowane następnie, jak również ustalenie liczb wygenerowanych wcześniej. W artykule pokazano jak użyć narzędzia z3 do ustalenia stanu generatora, co pozwoliło na „odgadnięcie” jaka liczba pseudolosowa została wygenerowana w Firefoksie przed trzema liczbami podanymi jako argument do programu.

– Michał Bentkowski, prowadzi szkolenia, realizuje  testy bezpieczeństwa