Mega Sekurak Hacking Party w Krakowie! 20.10.2025 r. Bilety -30%
Atak DoS na aplikacje – przez wyrażenia regularne
Amerykański programista, Jamie Zawinski, napisał kiedyś słynne słowa o wyrażeniach regularnych: “Niektórzy ludzie, gdy napotykają na problem, myślą sobie: »Wiem! Użyję wyrażeń regularnych«. I teraz mają dwa problemy”. W tym artykule przekonamy się jak prawdziwe są to słowa, jeżeli wyrażenie regularne zostało napisane w sposób niewłaściwy, umożliwiając tym samym przeprowadzenie ataku Denial-of-Service na aplikację.
Podstawy
Niniejszy akapit zawiera podstawy używania wyrażeń regularnych. Czytelnicy zaznajomieni z tematem mogą przeskoczyć od razu do kolejnej sekcji.
Wyrażenia regularne (regexy) pozwalają programistom określać wzorzec tekstu, a następnie sprawdzać czy dany ciąg znaków pasuje do tego tekstu. W praktycznych zastosowaniach często są używane do walidacji danych, na przykład: jeżeli mamy w aplikacji pole, w którym użytkownik powinien wpisać kod pocztowy, możemy sprawdzić jego poprawność wyrażeniem: ^[0-9]{2}-[0-9]{3}$. Regexy mogą zawierać zarówno zwykłe znaki, jak i znaki o znaczeniu specjalnym. Poniżej krótka ściągawka najczęściej używanych znaków o znaczeniu specjalnym:
- „.” (kropka) – dopasowuje dowolny znak,
- „^” – początek ciągu znaków,
- „$” – koniec ciągu znaków,
- „*” – wyrażenie regularne poprzedzające gwiazdkę może zostać powtórzony dowolną liczbę razy (także zero razy). Na przykład wyrażenie „ab*” dopasowuje między innymi „abb”, „ab” i „a”.
- „+” – wyrażenie regularne poprzedzające plus może zostać powtórzone co najmniej jeden raz. Tak więc „ab+” nie dopasuje już samego „a”,
- „{n}” – wyrażenie regularne musi zostać powtórzone dokładnie n razy,
- „[…]” – określa zbiór znaków, które mogą zostać dopasowane. Mogą one zostać zarówno wypisane jawnie, np. „[abz]” lub jako zakres: „[a-z]”. Jeżeli pierwszym znakiem zbioru jest „^” wówczas dopasowywane są znaki nie znajdujące się w zbiorze. Na przykład: „[^a-z]” dopasuje wszystkie znaki poza małymi literami alfabetu łacińskiego.
- „|” – odpowiednik operatora OR. Wyrażenie regularne „ab|cd” dopasuje ciąg znaków „ab” lub „cd”.
- „(…)” – grupowanie wyrażeń regularnych.
Przykładowo: jeżeli chcemy dopasować ciąg znaków zaczynający się od „Sekurak „ , gdzie następnie ma pojawić się ciąg znaków „2016” lub „2017” , a następnie dziesięć dowolnych cyfr, możemy to zapisać następująco: „^Sekurak (2016|2017)[0-9]{10}” .
Implementacje
W najpopularniejszych językach programowania, takich jak C# (ogólnie .NET), Python, PHP czy Java implementacja wyrażeń regularnych polega na zbudowaniu niedeterministycznego automatu skończonego (NFA). Jego działanie polega na czytaniu kolejnych tokenów z wyrażenia regularnego i dopasowywaniu ich w sprawdzanym ciągu znaków. Co istotne, domyślnie silniki regexów działają w trybie zachłannym, tj. dopasowywują tak dużo powtórzeń danego znaku jak tylko się da. Jeżeli silnik stwierdzi, że dany ciąg znaków nie pasuje do wyrażenia regularnego, wówczas stosowany jest backtracking, czyli powrót do takiego miejsca w regexie, w którym silnik mógł obrać inną ścieżkę wykonywania.
Zobaczmy to na przykładzie. Mamy wyrażenie regularne „a+.b” i próbujemy dopasować ciąg „aab”.
| Regex | Ciąg znaków | Komentarz |
| „a+.b” | „aab” | Silnik wyrażeń regularnych zaczyna od dopasowywania „a+”. W pierwszym kroku dopasowuje tak dużo znaków „a” jak tylko się da (wspomniany wyżej: tryb zachłanny). |
| „a+.b” | „aab„ | Kropka oznacza dowolny znak, stąd silnik dopasowuje go do litery „b”. |
| „a+.b„ | „aab„ | Silnik oczekuje teraz litery „b”, jednak napotyka na koniec ciągu znaków. Oznacza to, że w tym przypadku nie ma dopasowania, więc niezbędny jest backtracking – powrót do wcześniejszego miejsca w wyrażeniu regularnym, w którym dopasowanie mogło być inne. |
| „a+.b” | „aab” | Silnik wraca więc do początku i próbuje dopasować jedną literę „a” mniej. |
| „a+.b” | „aab” | Kropka tym razem jest dopasowana do litery „a”. |
| „a+.b„ | „aab„ | Na końcu regexa mamy literę „b”, mamy ją też na końcu ciągu znaków. Stąd silnik zwraca w odpowiedzi, że ten ciąg znaków pasuje do regexa. |
Nawet w takim stosunkowo prostym wyrażeniu regularnym i krótkim ciągu znaków widać, że za pierwszym razem silnik wyrażeń regularnych przyjął „niewłaściwą” ścieżkę dopasowywania go do ciągu znaków i musiał wrócić do wcześniejszego stanu, by móc stwierdzić, że dopasowanie istnieje. Innymi słowy – silnik sprawdza wszystkie możliwe sposoby dopasowania wyrażenia regularnego zanim wyda ostateczny wyrok czy dopasowanie istnieje.
Właśnie ta cecha silników może zostać nadużyta do wykonania ataku Denial-of-Service. Jeżeli wyrażenie regularne zostanie napisane w sposób niewłaściwy (zobaczymy poniżej przykład), to czas potrzebny na jego analizę może rosnąć wykładniczo.
„Złe” wyrażenia regularne
Weźmy wyrażenie regularne: „^(a+)+$”; mamy w nim literę „a”, która musi wystąpić co najmniej jeden raz, wpisana w grupę, która również musi wystąpić co najmniej raz. Jeżeli weźmiemy ciąg znaków, który pasuje do tego wyrażenia, jak np. „aaaaa”, to odpowiedź dostaniemy bardzo szybko, bowiem silnik regexów będzie w stanie od razu dopasować wszystkie litery „a”. Co jednak się stanie, gdy celowo użyjemy ciągu znaków, który nie zostanie dopasowany? Zobaczmy na przykładzie „aab”.
| „^(a+)+$” | „aab” | Silnik zaczyna od dopasowania początku ciągu znaków. |
| „^(a+)+$” | „aab” | Silnik sprawdza dopasowanie grupy. |
| „^(a+)+$” | „aab” | Silnik dopasowuje maksymalną możliwą liczbę liter „a”. |
| „^(a+)+$” | „aab„ | Za dopasowaniem grupy mogłoby znaleźć się kolejne dopasowanie grupy. Mamy jednak literę „b” stąd backtracking. |
| „^(a+)+$„ | „aab„ | Alternatywnie za literami „a” może być koniec ciągu. To również nie jest prawda, więc niezbędny jest backtracking. |
| „^(a+)+$” | „aab” | Silnik wraca do dopasowań litery „a” i dopasowuje jedną mniej. |
| „^(a+)+$” | „aab” | Kolejny raz sprawdzane będzie dopasowanie grupy. |
| „^(a+)+$” | „aab” | W drugiej grupie znajdzie się pojedyncze wystąpienie litery „a”. |
| „^(a+)+$” | „aab„ | Potencjalnie mogłaby wystąpić trzecia grupa. Jednak w niej nie będzie dopasowania, stąd backtracking. |
| „^(a+)+$„ | „aab„ | Końca ciągu znaków również nie ma, więc znów niezbędny byłby bactracking. Jednak silnik nie byłby już w stanie dopasować mniej liter „a”, więc w tym momencie może już zakończyć próby i zwrócić odpowiedź, że dopasowania nie ma. |
Jak widzimy próba dopasowania stosunkowo łatwego wyrażenia regularnego i krótkiego ciągu znaków wymagała mimo wszystko dość żmudnego sprawdzania wszystkich możliwości przez silnik. Jeżeli utworzylibyśmy ciąg znaków składający się z jednej litery „a” więcej, wówczas silnik potrzebowałby dwa razy więcej kroków, by stwierdzić, że wyrażenie regularne nie jest dopasowane. De facto analiza tego wyrażenia polega na próbie podzielenie liter „a” na grupy na wszystkie możliwe sposoby, nim zostanie zwrócony wynik. Czyli dla ciągu „aaaab”, silnik próbowałby następujących podziałów: „(aaaa)”, „(aaa)(a)”, „(aa)(aa)”, „(aa)(a)(a)”, „(a)(aaa)”, „(a)(aa)(a)”, „(a)(a)(aa)”, „(a)(a)(a)(a)”. Łatwo zauważyć, że gdy mamy n liter „a” to sprawdzanych jest 2n-1 możliwości.
Na rysunku 1. pokazany został przykład benchmarka z języka Python, w którym każde dodanie jednego znaku „a” przedłuża analizę wyrażenia regularnego dwukrotnie. Oczywiście dodanie kilkunastu bądź kilkudziesięciu znaków sprawiłoby, że analiza wyrażenia regularnego musiałaby zająć kilka dni, miesięcy czy lat. Uruchomienie tego na aplikacji webowej mogłoby spowodować unieruchomienie serwera.
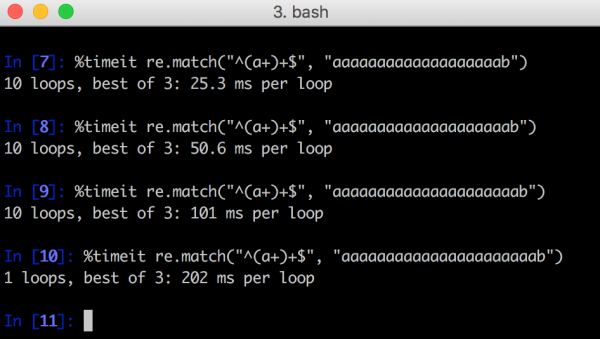
Rys 1. Przykład dopasowania regexa w Pythonie – analiza każdego kolejnego ciągu znaków zajmuje dwa razy dłużej.
Jak się bronić?
Wykrywanie czy dane wyrażenie regularne może być podatne na problem Denial-of-Service nie jest proste. Szczególnie trudno zauważyć problem w bardziej skomplikowanych regexach, np. dopasowujących adresy e-mail lub HTML. Lampka ostrzegawcza powinna się zawsze zapalać, jeżeli widzimy w wyrażeniu regularnym grupę, w której użyto dowolnego operatora powtórzenia, zaś w środku samej grupy również użyty został operator powtórzenia. Przykłady:
- „(a+)+”
- „(a+a+)+”
- „(x[a-z]+)*”
Jeżeli jest to możliwe, należy się wystrzegać tego typu regexów i postarać się je przepisać w inny sposób. Jednym ze sposobów na sprawdzenie czy wyrażenie regularne jest podatne na problem może być ułożenie ciągu znaków, który jest poprawny, a następnie dokonywanie w nim drobnych modyfikacji – i sprawdzanie w jaki sposób wpływają one na czas analizy.
W niektórych aplikacjach przewiduje się jednak, że użytkownik może sam wpisać wyrażenie regularne, np. w wyszukiwarce. Wówczas zaleca się, aby zdefiniować w aplikacji timeouty na wykonywanie wyrażeń regularnych. Na przykład w .NET od pewnego czasu timeouty w regexach są wspierane przez framework. Jeżeli używany przez nas język programowania nie dostarcza sam w sobie takiej opcji, niezbędna będzie ręczna implementacja.
Podsumowanie
Silniki wyrażeń regularnych w najpopularniejszych językach programowania są zaimplementowane jako niederministyczny automat skończony (NFA). Taka implementacja jest łatwa do zaprogramowania, jednak sprawia, że czas analizy pewnych wyrażeń regularnych rośnie wykładniczo w zależności od długości danych.
W wielu językach programowania nie ma wbudowanych zabezpieczeń przed tego typu atakami. Najbardziej uniwersalną metodą jest zaimplementowanie timeoutu na czas analizy wyrażenia regularnego.
Dalsza lektura
–Michał Bentkowski, realizuje testy bezpieczeństwa w Securitum.


Kolejny świetny tekst Michała, oby tak dalej!
Jak się bronić w PHP? max execution time wystarczy jako rozwiązanie zmniejszające dotkliwość skutków ataku?
Jak się bronić? A co masz takiego w tej swojej bazie danych, że odpytujący „musi” użyć wyrażeń regularnych? Od tego zacznij… Jak nie ma potrzeb używania wyrażeń regularnych, to waliduj tekst zapytania na obecność znaków niepożądanych. Co zbędne to wyrżnij z zapytania. Ja tak to widzę.
Tak, max_execution_time jest OK o ile nie przeszkadza Ci, że skrypt zostanie przerwany. Zakładam, że większości przypadków nie stanowi to problemu.
Bardzo ciekawe
„Amerykański programista, Jamie Zawinski”
Taaa ;D
Pewnie Hindus ;)
A co z ograniczeniem ilości wprowadzanych znaków wyrażenia do porównania ciągu z regexem?
Super artykuł! Zawsze mnie zastanawiało czy tworzenie oprogramowania szkodliwego bardzo różni się od zwykłego kodu. Dzięki za artykuł!
mam podejżenie jeszcze innego ataku na wp. Dostalem komenta, ucieszylem sie ale mial blędne czcionki.poprawilem.zablokowalo mi fonka… co o tym myślicie Sekuraki?