Konferencja Mega Sekurak Hacking Party w Krakowie – 26-27 października!
Algorytm Ring-LWE w Chrome do obsługi HTTPS – ochrona przed komputerami kwantowymi
Na oficjalnym blogu Google pojawiła się informacja o dodaniu do obsługi HTTPS w Chrome algorytmu Ring Learning With Errors. Wszystko to jako eksperyment służący przetestowaniu rozwiązania chroniącego przed łamaniem komunikacji z wykorzystaniem komputerów kwantowych.
Popularne algorytmy typu Diffie-Hellmann czy RSA mają pewne słabości jeśli chodzi o łamanie kwantowe, w przeciwieństwie do właśnie Ring-LWE. Niektórzy twierdzą nawet, że wykorzystanie komputerów kwantowych do skutecznego łamania klasycznych algorytmów asymetrycznych to kwestia 20-100 lat. Zatem część komunikacji, która obecnie jest zapisywana przez różne organizacje być może… będzie przełamana właśnie po tym czasie.
Obecnie algorytm ma być wspierany dla HTTPS pomiędzy Chrome a częścią serwerów Google.
Jeśli Wasza przeglądarka używa tego algorytmu, w DevTools na zakładce Security zobaczycie CECPQ1:
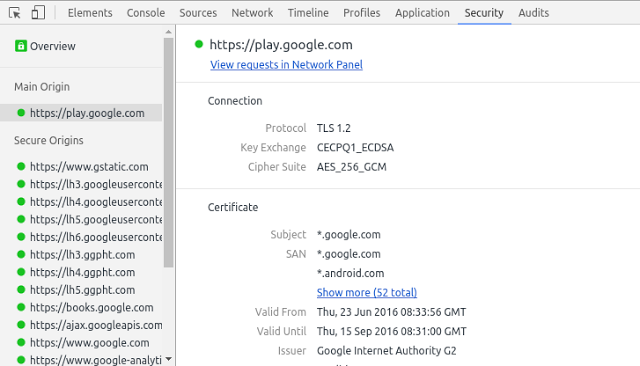
–Michał Sajdak


Hmm, myślę, a implementacja open source jakaś jest?
Let me google that for you zwraca
https://www.cecpq1.com/
tam papier
https://cryptojedi.org/papers/newhope-20160328.pdf
a w nim adres repo
https://github.com/tpoeppelmann/newhope
w avx2 i ref dwie wersje implementacji
Kolejny trop to code review do chromium
https://codereview.chromium.org/2012353002/
wprawdzie wprowadza tylko możliwość użycia nowych protokołów, ale ich nazwy trochę mówią o strukturze:
{0xc5, 0xc5b}, // TLS_DH_anon_WITH_CAMELLIA_256_CBC_SHA256
+ {0x16b7, 0x128f}, // TLS_CECPQ1_RSA_WITH_CHACHA20_POLY1305_SHA256 (exper)
+ {0x16b8, 0x138f}, // TLS_CECPQ1_ECDSA_WITH_CHACHA20_POLY1305_SHA256 (exper)
+ {0x16b9, 0x1277}, // TLS_CECPQ1_RSA_WITH_AES_256_GCM_SHA384 (exper)
+ {0x16ba, 0x1377}, // TLS_CECPQ1_ECDSA_WITH_AES_256_GCM_SHA384 (exper)
Widać, że CECPQ1 wskoczyło zamiast Diffie Hellmana, bo cała reszta normalna: RSA lub ECDSA, AES 256 lub CHACHA20 (patrz tu: https://en.wikipedia.org/wiki/Salsa20) i skrót na SHA256 lub 384.
W papierze wspomniane trzy działające implementacje, w tym na Cortex.
Jedna opisana w kolejnym papierze
http://eprint.iacr.org/2014/725.pdf
a w nim
tadam
http://homes.esat.kuleuven.be/~ssinharo/
a tu tylko podajesz dane osobowe Uniwersytetowi Katolickiemu w Leuven i link do kodu dostaniesz na mail.
Ciekawe kto się rejestrował, Brin czy Page?
Autorzy twierdzą, że motywacją ich pracy jest fakt, że za pomocą algorytmu Shora można teoretycznie łamać zarówno problem faktoryzacji (zwykły DH) jak i wersję eliptyczną (ECDH). Całę prezdsięwzięcie nazywa się proroczo New Hope.
Pzdr