Konferencja Mega Sekurak Hacking Party w Krakowie – 26-27 października!
Jedenastolatka sprzedaje bezpieczne hasła za 2 USD
Diceware to znana metoda generowania bezpiecznych i stosunkowo łatwych do zapamiętania haseł. Pomysł polega na utworzeniu długiego ciągu uwierzytelniającego składającego się z kilku losowo wyznaczonych słów. Zamiast wyznaczać je osobiście, tego typu hasła można zakupić od pewnej przedsiębiorczej jedenastolatki.
Jedenastoletnia Mira Modi zarabia na sprzedaży usług generowania bezpiecznych haseł — ręcznie wygenerowane i odręcznie zapisane hasło możemy nabyć w serwisie dicewarepasswords.com.
Za 2 USD otrzymamy ciąg uwierzytelniający składający się z 6 losowo wybranych słów — taką ilość uważa się obecnie za wystarczającą do typowych zastosowań.
Metoda Diceware określa, że każde ze słów zostaje wyznaczone spośród określonej listy słów za pomocą 5 niezależnych rzutów sześcienną kością do gry — tak otrzymany pięciocyfrowy ciąg wskazuje określone słowo na liście. By wygenerować hasło złożone z sześciu słów potrzeba więc 30 rzutów.
Taki ciąg słów jest przez dziewczynkę odręcznie zapisywany i wysyłany konwencjonalną pocztą:
The passwords are sent by US Postal Mail which cannot be opened by the government without a search warrant.
Wszystkim, którzy nie wierzą w dobre intencje jedenastolatki, nie ufają jej kościom do gry lub po prostu chcą zachować własne hasła tylko dla siebie, polecamy jednak własnoręczne wygenerowanie ciągu — warto dodać, że jest również dostępna polska lista słów.
Przy okazji tej intrygującej historii warto było przypomnieć sobie starą, lecz nadal skuteczną metodę generowania silnych i łatwych do zapamiętania haseł…
— Wojciech Smol


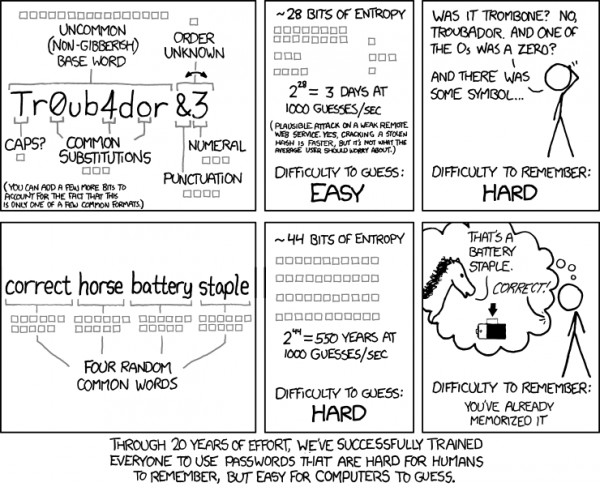

To ja lekko włożę z rana kij w mrowisko: jedyne hasła, które w ogóle powinno się pamiętać, to hasło logowania do stacji roboczej i do menedżera haseł. https://diogomonica.com/posts/password-security-why-the-horse-battery-staple-is-not-correct/
:)
BTW, język polski z jego bogactwem odmian daje przy tej metodzie całkiem spore pole do popisu.
Tak tak i zblokować dostęp do usług internetowych :) dlatego do Dropboxa też trzeba pamiętać i konta e-mail :)
Zaraz zaraz, ale jak ona rzuca sześcienną kostką, to to nie oznacza czasem, że najmniejsza kombinacja to 11111, a największa 66666? Dla marginesu błędu wystarczy użyć słów od 10000 do 70000 w dowolnym słowniku angielskiego i mamy hasło w jakieś 30 sekund :D Chyba jej wyślę jakiś generator liczb losowych opierających się na zmiennych, które będzie mogła podawać tak jak teraz z sześciennych kości + modyfikacja przez czas (w zakresie pełnego słownika 1-250k), żeby tych ludzi nie krzywdziła! ;p
Schneier już w marcu 2014 pisał: “This is why the oft-cited XKCD scheme for generating passwords — string together individual words like “correcthorsebatterystaple” — is no longer good advice. The password crackers are on to this trick.”
https://www.schneier.com/blog/archives/2014/03/choosing_secure_1.html
Metoda Diceware przewiduje w razie takiej potrzeby budowanie jeszcze bardziej złożonych haseł:
http://world.std.com/~reinhold/diceware.html
@Józek Twoje obliczenia są dobre do jednego słowa, a hasło ma ich 6.
5 rzutów/słowo (3125 możliwych słów) x 6 słów/hasło daje 6^30 ~~ 2^77 – i to przy założeniu, że dokładnie znamy użyty słownik.
Nie do końca tak to działa ;) wchodzisz na bardzo drażliwe tematy probabilistyki, gdzie wyrzucenie 5 razy 4 oczek przy 5 rzutach pod rząd to stosunkowo wysokie prawdopodobieństwo. Nie czepiam się samej metody tworzenia haseł, tylko metody losowania słów. Mógłbym zacząć liczyć i liczyć i udowodnić, że w ogromnej ilości przypadków słowa i ich ciągi będą zaraz na początku tablic, więc odpowiednio gdyby odpowiednio “rządzić i dzielić”, można bardzo szybko zyskiwać poprawne hasła (np. robiąc x/20 tablic), tylko po co? :D Losowe ciągi liter są dużo, dużo bardziej bezpieczne dlatego, że każda litera może być wylosowana w dowolnej pozycji tablicy, więc chcąc nie chcąc, musisz przeszukiwać całą tablicę z każdą kolejną iteracją od początku i tylko konkretny traf da ci poprawny wynik, a kombinacji masz 69^16 ;p W przypadku “tej” metody musisz jedynie przeszukiwać 5 tablic, gdzie każda posiada ok. 50 000 słów i dodatkowo, najprawdopodobniej każde słowo znajduje się blisko początku bądź końca tej tablicy (no ewentualnie blisko środka). Także jak widzisz, nawet sama metoda ma swoje potężne minusy ;)
(namąciłem coś? xD)