Czym jest atak kryptograficzny Bit-Flipping – teoria i praktyka

Tryb CBC

Wyjaśniając mechanizm przeprowadzenia ataku Bit-Flipping, w pierwszej kolejności musimy wytłumaczyć, w jaki sposób działa deszyfrowanie w trybie CBC.

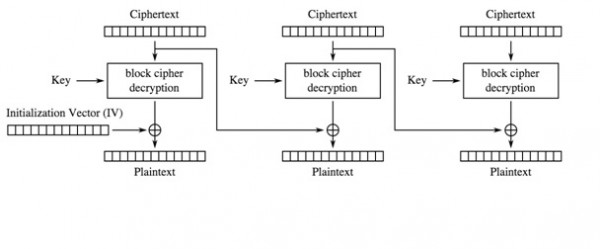
Rysunek 1. Schemat procesu deszyfrowania w trybie CBC (Wikipedia).

Szyfrogram składa się z bloków o stałej długości (8, 16 lub 32 bajtów), w naszym przykładzie posłużymy się najbardziej popularnym – 16-bajtowym. Do szyfrogramu dołączany jest IV czyli Initialization Vector, generowany podczas szyfrowania. To właśnie dzięki niemu szyfrowanie tych samych danych generuje różne szyfrogramy – tak długo, jak Initialization Vector (IV) jest różny.

Nasz szyfrogram wygląda więc w taki sposób:

[ Initialization Vector ] [ Blok 1 ] [ Blok 2] [Blok 3]

Pierwszym etapem deszyfrowania jest rozbicie szyfrogramu na bloki i wydzielenie bloku IV.

Blok jest deszyfrowany za pomocą klucza, a następnie poddawany procesowi xorowania z poprzednim blokiem szyfrogramu lub w przypadku bloku pierwszego z wartością IV (Initialization Vector).

Integralność CBC

Szyfrowanie CBC nie dostarcza żadnego mechanizmu, który dbałby o integralność danych, co sprawia, że modyfikując szyfrogram, wpływamy na wynikowy tekst jawny.

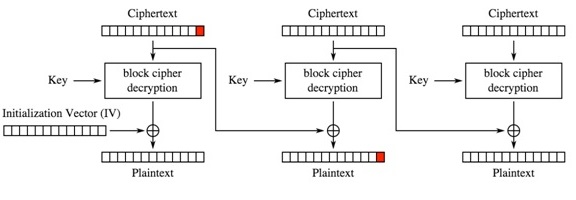
Rysunek 2. Schemat procesu deszyfrowania: zaznaczono ostatni bajt bloku.

Przejdźmy więc do prostego przykładu szyfrowania tekstu „Sekurak Party” za pomocą algorytmu AES w trybie CBC.

1. Do tekstu dodawany jest padding „Sekurak Party\x03\x03\x03” (w naszym wypadku PKCS #7 – można o tym więcej przeczytać w artykule Michała Bentkowskiego na temat padding Oracle),
2. Generowany jest 16-bajtowy Initialization Vector (IV),
3. Tekst jawny jest xorowany z IV i szyfrowany przy użyciu klucza szyfrującego,
4. Wynikowy szyfrogram wygląda następująco:

[ Initialization Vector ] [Blok 1]

W tym konkretnym przypadku, deszyfrowanie będzie wyglądać tak:

1. Szyfrogram zostanie rozbity na dwa bloki 16 bajtowe – IV oraz Blok 1,
2. Blok 1 przejdzie przez algorytm deszyfrowania przy użyciu klucza szyfrującego,
3. Wynikowy blok zostanie poddany xorowaniu z wartością IV i otrzymamy tekst jawny.

Bit-Flipping – przykładowy atak

Do przeprowadzenia ataku Bit-Flipping wymagana jest wiedza dotycząca tekstu jawnego konkretnego szyfrogramu. Mamy więc (opisany poniżej) prosty skrypt, który potraktujemy jak czarną skrzynkę. Należy pamiętać o niedekodowaniu klucza, chcemy przecież przeprowadzić atak bez jego znajomości.

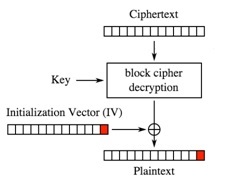
Rysunek 3. Deszyfrowanie pojedynczego bloku szyfrogramu.

Przyjrzyjmy się zatem przykładowemu skryptowi podatnemu na atak Bit-Flipping.

Listing 1. Skrypt podatny na atak Bit-Flipping.

#!/usr/bin/env python
import sys
from base64 import b64decode
from Crypto.Cipher import AES

def decrypt(cipher, key):
    IV = cipher[:16]
    cipher = cipher[16:]
    aes = AES.new(key, AES.MODE_CBC, IV=IV)
    plain = aes.decrypt(cipher)
    return plain

key = b64decode("WWVsbG93IFN1Ym1hcmluZQ==")
plain = decrypt(sys.argv[1].decode('hex'), key)
print repr(plain)

Skrypt przyjmuje jako argument szyfrogram zakodowany w postaci HEX-a, następnie przeprowadza proces deszyfracji i wyświetla tekst jawny.

Załóżmy więc, że tekstowi jawnemu „Sekurak Party\x03\x03\x03” odpowiada szyfrogram (szyfrogram został zakodowany w formie heksadecymalnej, na czerwono zaznaczono natomiast Initialization Vector):

6ca79ad332213699f3f0bf8b50bb3a19f8c17dcd69a95b8dc3bf92bc88d024d3

Rysunek 4. Działanie skryptu.

Wiedząc, że ostatni bajt to „\x03” i że jest on wynikiem operacji XOR „\x19” (ostatni bajt IV) z jakimś X (oczywiście można w prosty sposób wyliczyć jego wartość, choć nie ma takiej potrzeby):

0x19 ^ X = 0x03

Aby jako wynik otrzymać 0x1, musimy poddać procesowi xorowania w pierwszej kolejności obie strony równania przez wartość 0x03:

0x19 ^ X ^ 0x03 = 0x00

A następnie przez wartość 0x1:

0x19 ^ X ^ 0x03 ^ 0x01 = 0x01

Jak widać, cały algorytm sprowadza się do wykonania operacji XOR ostatniego bajtu IV – w pierwszej kolejności przez ostatni bajt tekstu jawnego następnego bloku, a następnie przez wartość, na jaką chcemy docelowy bajt zmienić.

Ostatni bajt IV musi więc zostać zamieniony na wartość:

0x19 ^ 0x03 ^ 0x01 = 0x1b
6ca79ad332213699f3f0bf8b50bb3a1bf8c17dcd69a95b8dc3bf92bc88d024d3

Tak utworzony szyfrogram przekazujemy do naszego skryptu czarnej skrzynki:

Rysunek 5. Działanie skryptu.

Tekst jawny rzeczywiście został zmodyfikowany bez znajomości klucza szyfrującego.

Proces jest na tyle prosty, że możemy stworzyć skrypt, który wygeneruje nowy Initialization Vector pozwalający zmienić wartość całego tekstu jawnego.

Aby zamienić ciąg „Sekurak Party\x03\x03\x03” na ciąg „Sekurak Hacking\x01” należy dokonać operacji XOR na odpowiednich bajtach bloku poprzedzającego – w tym wypadku IV.

Listing 2. Skrypt przeprowadzający atak Bit-Flipping.

def xor(a, b):
    res = ""
    for i in range(0, len(a)):
        res += chr(ord(a[i]) ^ ord(b[i]))
    return res

cipher = "6ca79ad332213699f3f0bf8b50bb3a19f8c17dcd69a95b8dc3bf92bc88d024d3".decode('hex')
IV = cipher[:16]
old = "Sekurak Party\x03\x03\x03"
new = "Sekurak Hacking\x01"

# nowe IV
newiv = xor(IV, xor(new, old))

print "Nowe IV: %s" % newiv.encode('hex')
print "Nowy szyfrogram: %s" % (IV + cipher[16:]).encode('hex')

Wynik działania skryptu:

Rysunek 6. Atak Bit-Flipping.

Nowo powstały szyfrogram możemy załadować do algorytmu deszyfrującego, co zwróci nam wartość „Sekurak Hacking\x01”.

Rysunek 7. Zmodyfikowany tekst jawny.

Zdobywanie informacji dotyczących tekstu jawnego

Jak wspominałem wcześniej, próbujemy zdobyć wiedzę dotyczącą tekstu jawnego dla konkretnego szyfrogramu. Te informacje możemy zdobyć na trzy sposoby:

1. przeprowadzając atak padding oracle,
2. korzystając z pewnej znajomości formatu danych,
3. modyfikując bajty w szyfrogramie i obserwując wyjścia aplikacji.

Pierwszy sposób został świetnie opisany przez Michała Bentkowskiego, dlatego odsyłam do jego artykułu. Druga metoda to wiedza o tym, jaki format mogą przyjąć dane. Takim przykładem może być format JSON, który składa się z klamr, cudzysłowów oraz znaków dwukropka.

Skupmy się więc na sposobie trzecim, czyli modyfikacji bajtów i obserwacji wyjścia aplikacji.

Praktyczny atak

Przeprowadzimy bardziej praktyczny atak, którego celem będzie pozyskanie poufnych danych.

Nieco zmodyfikowany skrypt czarnej skrzynki:

Listing 3. Skrypt wczytujący plik na podstawie zaszyfrowanego ciągu.

#!/usr/bin/env python
import sys
import json
from base64 import b64decode
from Crypto.Cipher import AES

def decrypt(cipher, key):
    IV = cipher[:16]
    cipher = cipher[16:]
    aes = AES.new(key, AES.MODE_CBC, IV=IV)
    plain = aes.decrypt(cipher)
    return plain

key = b64decode("WWVsbG93IFN1Ym1hcmluZQ==")
plain = decrypt(sys.argv[1].decode('hex'), key)

try:
    res = json.loads(plain)
    print 'Reading %s...' % res['f']
    f = open(res['f'], 'r')
    print '------------------\n%s\n------------------' % f.read()
    f.close()
except:
    sys.exit(1)

Uruchamiamy skrypt, przekazując jako argument następujący ciąg:

0ec9a5b6a8304467899fda07d9eb15b741b186a4d266bb671927ae1e609389bd

Rysunek 8. Odczytanie pliku „test.txt”.

Wyjście aplikacji wskazuje, że czytana jest treść pliku “test.txt”.

Co się jednak stanie, jeżeli zaczniemy “flippować” bity w bloku IV dla konkretnych bajtów, zaczynając od końca?

Szyfrogram:

0ec9a5b6a8304467899fda07d9eb15b841b186a4d266bb671927ae1e609389bd

Rysunek 9. Modyfikacja kolejnego bajtu szyfrogramu.

Szyfrogram:

0ec9a5b6a8304467899fda07d9eb16b741b186a4d266bb671927ae1e609389bd

Rysunek 10. Modyfikacja kolejnego bajtu szyfrogramu.

Szyfrogram:

0ec9a5b6a8304467899fda07d9ec15b741b186a4d266bb671927ae1e609389bd

Rysunek 11. Modyfikacja kolejnego bajtu szyfrogramu.

Możemy więc wnioskować, że modyfikując zaznaczone w szyfrogramie bajty, jesteśmy w stanie zmienić całkowicie wartość test.txt. Na czerwono został zaznaczony fragment ciągu, pod którym kryje się zaszyfrowany tekst „test.txt”:

0ec9a5b6a8304467899fda07d9eb15b741b186a4d266bb671927ae1e609389bd

Aby zmienić wartość test.txt na flag.txt musimy wykonać operację XOR:

4467899fda07d9eb ^ hex(“test.txt”) ^ hex(“flag.txt”) = 566e9b8cda07d9eb

W efekcie otrzymujemy szyfrogram:

0ec9a5b6a830566e9b8cda07d9eb15b741b186a4d266bb671927ae1e609389bd

Po załadowaniu szyfrogramu do atakowanego skryptu zwracana jest treść pliku „flag.txt”:

Rysunek 12. Poufne informacje pozyskane za pomocą ataku Bit-Flipping.

Bez znajomości klucza udało się zmienić tekst jawny z „test.txt” na „flag.txt” i przeczytać sekretne dane.

Ograniczenia ataku Bit Flipping

Atak Bit-Flipping ma spore ograniczenia. Poprzednie przykłady były stosunkowo proste i składały się tylko z dwóch elementów – IV oraz pierwszego bloku.

Co stanie się w przypadku, gdy zaszyfrowany ciąg jest znacznie dłuższy i tworzy szyfrogram składający się z kilku bloków?

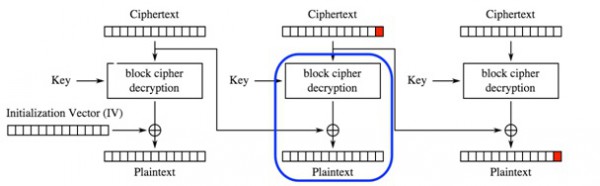
Rysunek 13. Deszyfrowanie kolejnych bloków szyfrogramu.

Jeżeli zaczniemy flippować bity w bloku 2, tak aby zmienić tekst jawny w bloku 3 (zaznaczone na czerwono), to szyfrogram w bloku 2 po deszyfrowaniu utworzy całkowicie inny tekst jawny w bloku 2. Takie zachowanie może prowadzić do błędu w przypadku, gdy w bloku 2 znajdowały się istotne dane – jak chociażby nazwy zmiennych czy zmiana formatu danych, np. “zepsucie JSON-a”.

Sposób obejścia ograniczenia

Jeżeli mamy możliwość modyfikacji danych, które są szyfrowane (np. username użytkownika), możemy spróbować ustawić ich długość oraz lokalizacje w taki sposób, aby “zepsuty blok” nadpisywał ich wartość.

Czyli, jeżeli szyfrowane dane wyglądają w taki sposób:

{“login”:”test”,“admin”:false}\x02\x02

utworzony szyfrogram da 2 bloki, które zostaną poprzedzone przez IV.

[ IV ] [{"login":"test",] ["admin":false}\x02\x02]

Flippowanie bitów w bloku [{„login”:”test”,] spowoduje jego deformacje i w efekcie zepsucie formatu JSON. Można jednak utworzyć konto z na tyle długim loginem, że jego część będzie stanowiła modyfikowany blok.

Rejestrujemy więc konto z loginem “AAAAAABBBBBBBBBBBBBBBB”, co spowoduje że aplikacja zaszyfruje taki ciąg:

{“login”:”AAAAAABBBBBBBBBBBBBBBB”,“admin”:false}

Ciąg zostanie rozbity na cztery 16-bajtowe bloki (IV + 3 bloki)

[ IV ] [{"login":"AAAAAA] [BBBBBBBBBBBBBBBB] [","admin":false}]

Dzięki temu, możemy modyfikować blok [BBBBBBBBBBBBBBBB], nie psując tym samym formatu JSON – oczywiście jeżeli nie pojawią się tam znaki, które w stringu znaleźć się nie powinny. Zainteresowanych odsyłam do standardu opisującego format JSON.

Podsumowanie – zalecane metody obrony

Zalecaną metodą zabezpieczenia przed atakiem Bit-Flipping jest dbanie o integralność szyfrogramu przez dodanie klucza HMAC i jego weryfikację przed deszyfracją danych.

Należy przyjąć zasadę, że nigdy nie powinno się wykonywać operacji kryptograficznych na nieuwierzytelnionych danych.

–Marcin Bury, pentester w Securitum