Czym jest Padding Oracle? – atak i ochrona

W tym artykule omówimy, czym jest Padding Oracle, oraz przedstawimy schemat ataku wraz z metodami obrony.

Zacznijmy jednak od podstaw. Najpopularniejsze obecnie algorytmy szyfrujące, takie jak AES czy 3DES, działają, bazując na blokach o stałych wielkościach. Na przykład: AES jest zdefiniowany do szyfrowania bloków o wielkości 128 bitów (16 bajtów). Oznacza to, że jeżeli chcemy zaszyfrować dane o dowolnej wielkości, musimy zadbać o to, by do funkcji szyfrującej przekazać je w postaci 16-bajtowych bloków.

Pojawiają się zatem zasadnicze pytania:

• Co zrobić, gdy mamy dane krótsze niż 16 bajtów? W jaki sposób wypełnić pozostałe bajty?
• Co zrobić, gdy mamy dane większe niż 16 bajtów? W jaki sposób podzielić je na bloki? W jaki sposób szyfrować poszczególne bloki?

Odpowiedzi na te pytania zamieszczam w dalszej części artykułu. Zapraszam do lektury

Padding – PKCS#7

Zacznijmy od ustalenia, co zrobić z danymi niebędącymi wielokrotnością wielkości bloku danego algorytmu. Na potrzeby przykładów założymy, że będziemy używać algorytmu AES, więc bloki będą miały 16 bajtów i chcemy zaszyfrować ciąg znaków „Programista”. Ponieważ mamy tylko 11 znaków, musimy czymś wypełnić pozostałe 5 znaków, by móc użyć AES-a. Innymi słowy – musimy użyć paddingu. Najczęściej używanym schematem paddingu jest standard PKCS#7, zdefiniowany w RFC 5652. Algorytm jest prosty – polega bowiem na tym, aby do szyfrowanego ciągu znaków dopisać bajty, których wartość jest równa liczbie brakujących bajtów do wielkości bloku.

Wracając do przykładu ciągu znaków „Programista” – do pełnego bloku brakuje 5 bajtów, stąd ten ciąg wraz z paddingiem, wygląda następująco: „Programista\x05\x05\x05\x05\x05”. Co istotne, jeżeli zdarzy się, że ciąg znaków, który chcemy zaszyfrować, jest już wielokrotnością wielkości bloku – należy wówczas dodać nowy blok – zawierający wyłącznie padding. Na przykład „Programista 2016” wraz z paddingiem to: „Programista 2016\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10” Wynika to z faktu, iż algorytm deszyfrujący oczekuje, że na końcu szyfrowanej wiadomości znajdzie się jakiś padding. Brak dodatkowego bloku z samym paddingiem wywołałby błąd podczas deszyfrowania.

Sposoby łączenia bloków zaszyfrowanych

Kolejny problemem, z którym musimy się zmierzyć, chcąc używać algorytmów szyfrujących, jest sposób łączenia bloków. Najprostszym sposobem szyfrowania danych większych niż 16 bajtów, byłoby podzielenie ich na bloki o długości 16 bajtów każdy i szyfrowanie każdego z nich osobno. Taki tryb pracy znany jest jako ECB (ang. Electronic CodeBook, rysunek 1).

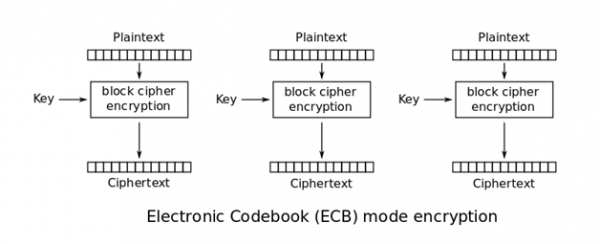
Rysunek 1. Sposób działania szyfrowania ECB (źródło: Wikipedia).

Zaletą tego trybu pracy jest jego wydajność – szyfrowanie każdego bloku jest niezależne, co pozwala na łatwe zrównoleglenie zarówno procesu szyfrowania, jak i deszyfrowania. Istotną wadą jest jednak fakt, że dla pewnych typów danych łatwo dostrzec wzorce, co sprawia, że szyfrowanie staje się nieefektywne. Najsłynniejszym na to przykładem jest szyfrowanie bitmapy przedstawiającej linuksowego pingwina (rysunek 2). Pomimo użycia silnego algorytmu szyfrującego dla poszczególnych bloków, wynik końcowy ewidentnie wskazuje, jaki obraz został zaszyfrowany (rysunek 3).

Rysunek 2. Tux przed szyfrowaniem (autor obrazka: lewing@isc.tamu.edu).

Rysunek 3. Tux zaszyfrowany w trybie ECB (autor obrazka: lewing@isc.tamu.edu).

Demaskuje to najistotniejszą wadę ECB – te same bloki danych tworzą ten sam szyfrogram. W danych binarnych często może to być strumień null-bajtów.

Aby rozwiązać ten problem, powstało wiele innych sposobów łączenia szyfrowanych bloków danych. Najpopularniejszym z nich (a zarazem tym, w którym pojawia się Padding Oracle) jest CBC (ang. Cipher Block Chaining). Na rysunku 4 przedstawiony jest schemat deszyfrowania danych w CBC.

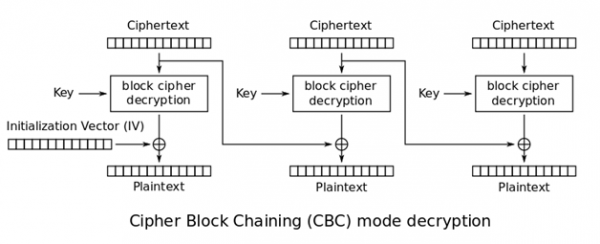
Rysunek 4. Deszyfrowanie danych CBC (źródło: Wikipedia).

W CBC szyfrogram każdego bloku jest zależny od poprzedniego. Aby zaszyfrować dane danego bloku, musimy najpierw wykonać operację XOR na tekście jawnym danego bloku oraz szyfrogramu poprzedniego bloku. Z kolei w przypadku deszyfracji – najpierw deszyfrujemy dane, używając algorytmu szyfrującego, a na wyniku tej operacji przeprowadzamy XOR z tekstem jawnym poprzedniego bloku. Specjalnym przypadkiem jest pierwszy blok, dla którego nie można przeprowadzić XOR-a z poprzednim blokiem. Zamiast tego, używa się tzw. wektora inicjalizacyjnego (IV – Initialization Vector). Dzięki takiemu sposobowi łączenia bloków, zmiana choćby jednego bajtu w tekście jawnym (zakładając, że używamy odpowiedniego algorytmu szyfrującego) wpływa na zmianę wszystkich kolejnych bloków w szyfrogramie.

Padding Oracle

Okazuje się, że sposób działania CBC pozwala na specyficzny dla tego trybu atak, czyli Padding Oracle. Aby można było taki atak wykonać, muszą być spełnione dwa warunki:

1. aplikacja musi pozwalać użytkownikowi na podanie własnego szyfrogramu,
2. aplikacja musi w jakiś sposób sygnalizować błędy paddingu.

Warunek pierwszy można spełnić dość łatwo – np. w aplikacjach webowych, często szyfrowane są wartości ciasteczek bądź niektórych parametrów GET/POST. Drugi warunek także często może być spełniony, jeżeli w aplikacji jest włączone wyświetlanie wyjątków. Praktycznie każda technologia, w której udostępniono metody do szyfrowania CBC, zasygnalizuje błąd (wyjątek), jeżeli po deszyfracji danych zostanie wykryty błąd paddingu. Błąd ten pojawia się, gdy padding nie jest zgodny z oczekiwanym. Na przykład, we wcześniejszym przykładzie mieliśmy paddingowany ciąg znaków „Programista\x05\x05\x05\x05\x05”. Gdyby w wyniku deszyfrowania danych, aplikacja otrzymała ciąg np. „Programista\x05\x05\x05\x05\x04”, wyświetliłaby błąd o niepoprawnym paddingu.

Treść błędu zależy od konkretnej technologii, np. w .NET zobaczymy błąd „Padding is invalid and cannot be removed”, zaś w Javie będzie to po prostu „Bad padding”.

Gdy spojrzymy ponownie na rysunek 4, możemy zauważyć, że tekst jawny każdego bloku zależy de facto od dwóch elementów: wyniku funkcji deszyfrującej dla tego bloku oraz szyfrogramu bloku poprzedniego.

Przyjmijmy następujące oznaczenia:

• C[i] – szyfrogram i-tego bloku (ciphertext),
• P[i] – tekst jawny i-tego bloku (plaintext),
• D() – funkcja deszyfrująca pojedynczy blok,
• ^ – operacja XOR.

Z diagramu wprost wynika, że P[i] = C[i-1] ^ D(C[i]). Zauważamy, że nad szyfrogramami mamy kontrolę, a więc możemy wpłynąć na C[i-1], co w konsekwencji pozwala wpłynąć na P[i]. Oczywiście zwykle nie wiemy, jaka jest wartość P[i] oraz co wychodzi z D(C[i]), jednak dzięki odpowiedniej analizie błędów paddingu będziemy w stanie to zrobić.

W pierwszej kolejności, będziemy chcieli tak ustawić wartość C[i-1], aby w wyniku działania algorytmu deszyfrującego nie został zwrócony błąd paddingu. W tym celu, będziemy zmieniać wartość ostatniego bajtu tego bloku na kolejne bajty od „\x00” do „\xff” z pominięciem oryginalnego bajtu C[i-1][15].

Na potrzeby przykładu załóżmy, że:

• C[i-1] = „abcdabcdabcdabcd”
• C[i] = 'Ob\xec\x1b\x18Ug5\x08\xa9\xc4\x9d\xec\x13R\x9d’

Zaczynamy więc od prób wpisywania kolejnych bajtów na ostatniej pozycji w C[i-1].

• ’abcdabcdabcdabc\x00′
• ’abcdabcdabcdabc\x01′
• ’abcdabcdabcdabc\x02′
• itp. …

Okazuje się, że dla C’[i-1]=’abcdabcdabcdabcf’ nie otrzymamy błędu paddingu.

Zastanówmy się teraz, jakie możemy wyciągnąć z tego wnioski?

Otóż błąd paddingu na pewno nie pojawi się, gdy P’[i][15]=”\x01″ ponieważ jest to jednobajtowy padding, a więc pojedyncza wartość „\x01” jest dla niego poprawna (co ciekawe, pewne implementacje akceptują także padding „\x00”, np. hurlant – biblioteka kryptograficzna dla ActionScript). Idąc dalej – jeśli zmodyfikujemy nasz wzór w taki sposób, by odnieść go tylko do ostatniego bajtu bloku, mamy: P’[i][15] = C’[i-1][15] ^ D(C[i])[15].

Zauważmy, że w równaniu składającym się z trzech elementów – wartości dwóch z nich znamy! Możemy więc obliczyć ostatni składnik wg wzoru:

D(C[i])[15] = P’[i][15] ^ C’[i-1][15]
D(C[i])[15] = "\x01 ^ "f"
D(C[i])[15] = "g" (0x67)

Voilà! Wiemy, jaki jest ostatni bajt wychodzący z funkcji deszyfrującej. Uzbrojeni w tę wiedzę, wracamy do oryginalnej wartości ostatniego bajtu bloku C[i-1] – a więc „d”. Wracamy do pierwotnego wzoru:

P[i][15] = C[i-1][15] ^ D(C[i])[15]
P[i][15] = "d" ^ "g"
P[i][15] = "\x03"

W ten sposób udało nam się zdeszyfrować oryginalną wartość ostatniego bajtu bloku!

Jest to „\x03″, co wskazuje na to, że w bloku jest trzybajtowy padding. Spróbujemy to potwierdzić, deszyfrując przedostatni bajt bloku.

W pierwszym kroku staraliśmy się znaleźć taką wartość ostatniego bajtu C[i-1], dla której P’[i-1][15]=”\x01”. W drugim kroku natomiast, będziemy się starali wymusić dwubajtowy padding, a więc spełnione będą następujące warunki:

• P’[i][15] = „\x02”
• P’[i][14] = „\x02”

Wykorzystując wiedzę z poprzedniego kroku, jesteśmy już w stanie ustalić takie C’[i-1][15], by otrzymać oczekiwany P’[i][15]. Mianowicie:

C’[i-1][15] = P’[i][15] ^ D(C[i])[15]
C’[i-1][15] = "\x02" ^ "g"
C’[i-1][15] = "e"

Z kolei, aby ustalić wartość C’[i-1][14], będziemy musieli robić to samo, co poprzednio, a mianowicie – próbować wszystkich możliwych wartości oprócz oryginalnej, czyli kolejno:

• C’[i-1] = 'abcdabcdabcdab\x00e’
• C’[i-1] = 'abcdabcdabcdab\x01e’
• itd. …

Tym razem okaże się, że błędu paddingu nie otrzymamy dla „abcdabcdabcdabbe”. Powtarzamy więc kroki z wyciągania ostatniego bajtu:

D(C[i])[14] = P’[i][14] ^ C’[i-1][14]
D(C[i])[14] = "\x02" ^ "b"
D(C[i])[14] = "`"

Wiemy już, jaki wynik dała funkcja deszyfrująca na przedostatnim bajcie, spróbujmy więc ustalić wartość tekstu jawnego dla tego bajtu:

P[i][14] = C[i-1][14] ^ D(C[i])[14]
P[i][14] = "c" ^ "`"
P[i][14] = "\x03"

Potwierdziliśmy więc, że przedostatnim bajtem jest w istocie „\x03”. Wyciąganie kolejnych bajtów odbywa się w analogiczny sposób:

1. chcąc wyciągnąć bajt trzeci od końca, musimy tak ustalić trzy ostatnie bajty, by padding wynosił „\x03\x03\x03”,
2. chcąc wyciągnąć bajt czwarty od końca, musimy tak ustalić cztery ostatnie bajty, by padding wynosił „\x04\x04\x04\x04” itd.

Chętnych do przećwiczenia Padding Oracle zapraszam do wykonania trzeciego zadania dostępnego pod tym adresem: https://rozwal.to/zadanie/20.

Metody ochrony

Zobaczyliśmy, w jaki sposób używanie trybu CBC do szyfrowania i wyświetlania błędów paddingu może pozwolić na deszyfrację danych – bez znajomości klucza szyfrującego.

Jak się zatem obronić przed tego typu atakami?

Przede wszystkim należy zadbać o to, aby aplikacja nie wyświetlała wyjątków wskazujących wyraźnie na błędy w paddingu. Ujawnianie tego typu informacji znacząco ułatwia przeprowadzanie ataków. Należy jednak pamiętać, że nawet jeśli błąd nie jest wprost wyświetlany, w pewnych sytuacjach można wywnioskować, że taki błąd wystąpił (np. serwer odpowiada kodem 500).

Z tego powodu zalecaną metodą ochrony jest dodawanie kodu MAC razem z zaszyfrowanymi wiadomościami. Można w tym celu użyć funkcji HMAC-SHA256. Przed przystąpieniem do deszyfrowania danych sprawdzamy najpierw, czy klucz HMAC-SHA256 pasuje do danych. Jeżeli nie – natychmiast odrzucamy żądanie. Dzięki temu, przeprowadzenie ataku nie będzie możliwe, bowiem niemożliwym będzie wygenerowanie poprawnego klucza.

Podsumowanie

Padding Oracle to atak, który dotyczy danych szyfrowanych w trybie CBC. Ze względu na specyficzne właściwości tego trybu, jak i najpopularniejszego schematu paddingu, możliwe jest deszyfrowanie danych niezależnie od tego, jak silny jest algorytm szyfrujący.

Zalecaną metodą zabezpieczenia się przed takim atakiem, jest dodawanie klucza HMAC do szyfrowanych danych – i sprawdzanie go przed przystąpieniem do deszyfracji.

Linki:

[1]: RFC 5652, definicja PKCS#7

–Michał Bentkowski, pentester w Securitum